
Related: What is a Good R-squared Value? Example: Find & Interpret R-Squared in R
GRAPH R SQUARED VALUE HOW TO
This tutorial provides an example of how to find and interpret R 2 in a regression model in R. In contrast, if we build a model for a physical process with very precise measurements, the R-squared values will naturally be high.The coefficient of determination (commonly denoted R 2) is the proportion of the variance in the response variable that can be explained by the explanatory variables in a regression model.
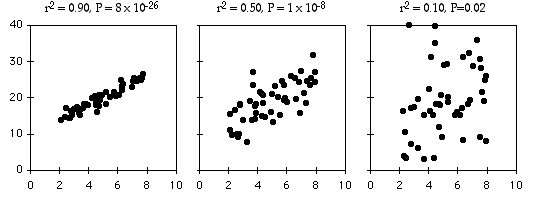
For instance, if we need to build a model on preferences of people on certain objects, there can be a lot of noise or variation in the data and therefore, one should not expect a high R-squared from such models. If you need to answer the question, how much R-squared is good enough, consider the context in which the analysis is being done. Also, do not get driven by a very high or very low R-squared value.
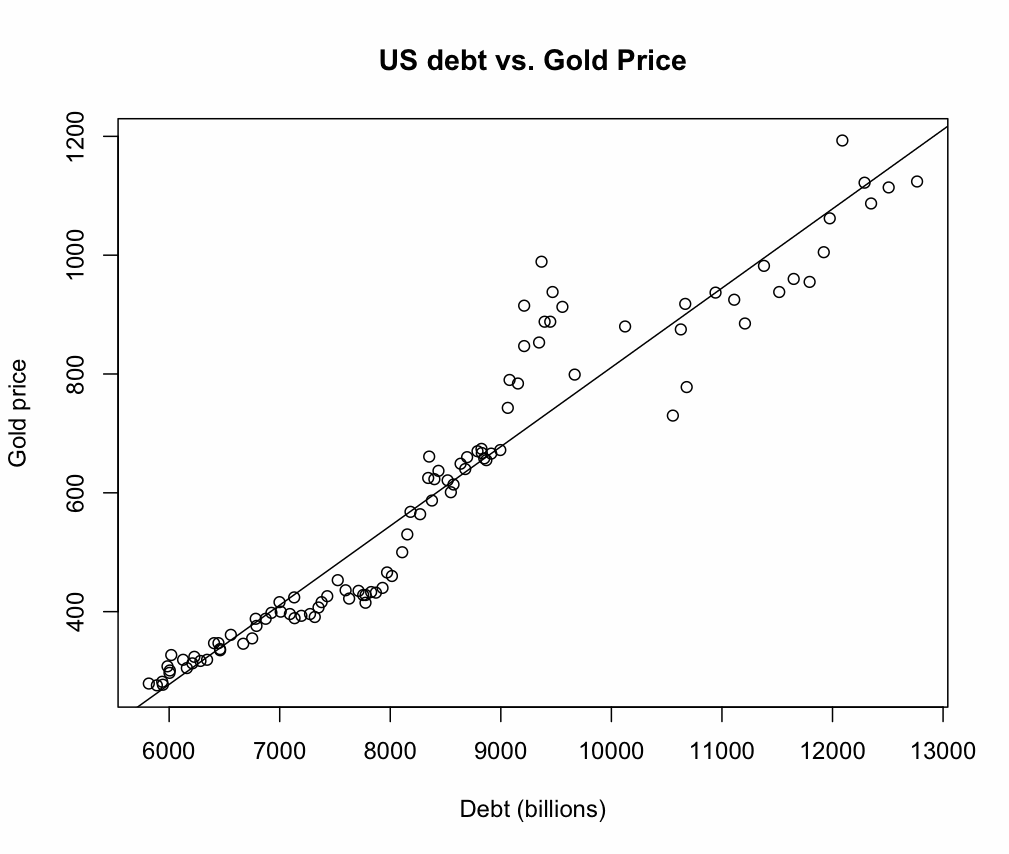
Avoid using R-squared for the purpose of model comparison. To summarize, before reaching any conclusion about the goodness of fit of the model solely on the basis of high or low R-squared value, consider plotting the data. Therefore, it is always advisable to plot the data to investigate whether the model assumption of linearity is met and not only rely on the R-squared values to arrive at a conclusion about the model. The relationship between x and y here is non-linear thus the model is wrong but the value of R-squared is more than 0.80, which is quite high.
GRAPH R SQUARED VALUE CODE
To explain this, let’s take a very crude example and generate a non-linear data using the R code given below and then perform a regression analysis on that: Sometimes it may happen that the model under consideration in not a linear model and the R-squared value comes out to be quite high. R-squared can be quite high even though the model is wrong If our main goal is to determine which predictors are important and how changes in the predictors affect the change in the outcome or the response variable, R-squared can be redundant. So, in this case a low R-squared does not really make your model meaningless. But in spite of this, the fitted line can show a significant trend which is being indicated by the low p-values of the predictors. Therefore, the data points are scattered away from the fitted regression line. The reason for low R-squared might be the data being used is highly variable and noisy. Does is mean that the significant predictors are meaningless?

The problem of low R-squared and significant predictorsĬonsider a situation where your predictors in the model turn out to be significant but the model has a low R-squared value. However, there are better tools available for model comparison viz., Information Criteria and Bayes’ Factors etc. Of course, instead of R-squared one may use adjusted R-squared for this purpose. One reason for this is the same that we have discussed in the above section that R-squared always favors the more complex model. However, R-squared should be avoided for comparing models. Given the simplicity of R-squared, sometimes researchers get tempted to use it for model comparison. Typically, the more non-significant predictors are added in the model, the more will be the gap between R-squared and Adjusted R-squared. Therefore, if you are dealing with a linear regression model with multiple predictors, it is always suggested to prefer Adjusted R-squared instead of R-squared to check the goodness of fit of the model. The adjusted R-squared penalizes the model for the addition of variables and increases only if the new added predictor actually affects the response variable. This means that R-squared will always favor the model with more predictors. A solution to this problem can be found in adjusted R-squared.
If you keep on adding the predictors to the model, the value of R-squared will increase, irrespective of the fact that the added predictors are important or not. R-squared increases with addition of more predictors This article highlights some of those issues with R-squared, and the motivation of this article is driven by several communications that I have had with different clinical teams during my statistical consultancy. Even though the concept of R-squared sounds very intuitive, it has some serious caveats. Given this logic, higher the R squared, the more variation is explained and hence one may consider the model to be better. So, an R-squared of 0.75 means that the predictors explain about 75% of the variation in our response variable. R-squared is defined as the percentage of the response variable variation that is explained by the predictors in the model collectively. To keep it simple, R-squared is a statistical measure which shows how close the data are to the fitted regression line. It gives a measure of goodness of fit for a linear regression model. R-squared, also known as coefficient of determination, is a commonly used term in regression analysis.


 0 kommentar(er)
0 kommentar(er)
